Achieving Efficient Tensor Contractions with a New Cost-Function-Based Greedy Algorithm
Tensor contractions play a crucial role in solving problems across various research fields, including model counting, quantum circuits, graph problems, and machine learning. However, finding an optimal contraction order is essential to minimize computational costs. The choice of contraction path greatly affects the efficiency of the computation, and researchers have been exploring different approaches to enhance tensor contraction paths.
In this article, we will delve into the topic of enhancing tensor contraction paths using a modified standard greedy algorithm with an improved cost function. We will explore the existing approaches, the limitations they face, and how the proposed method addresses these challenges to achieve more efficient tensor contractions.
The Significance of Tensor Contraction Paths
To understand the importance of tensor contraction paths, let’s consider the computation of the product of a sequence of matrices A, B, and C. The result of the computation will always be the same, but the computational costs may vary based on the dimensions of the matrices involved. The more tensors involved in a tensor network, the more the cost of contraction scales. Therefore, finding an efficient contraction path becomes crucial in minimizing the overall computation time.
Efficient tensor contraction paths have been the subject of extensive research. Several existing methods have been proposed to tackle this problem. Some of these methods include simulated annealing, genetic algorithms, graph decomposition techniques, and even reinforcement learning combined with graph neural networks.
Existing Approaches for Finding Contraction Paths
Simulated Annealing and Genetic Algorithms
One approach to finding efficient tensor contraction paths is through the use of simulated annealing and genetic algorithms. These methods outperform the standard greedy approach for smaller networks. Simulated annealing is a metaheuristic search algorithm that simulates the annealing process in materials. Genetic algorithms, on the other hand, are inspired by the process of natural selection and mimic evolutionary processes to find optimal solutions.
Graph Decomposition Techniques
Graph decomposition techniques, such as Line-Graph (LG) and Factor-Tree (FT) methods, have also been employed to compute tensor contraction paths. LG utilizes structured graph analysis to determine the optimal contraction order. FT, on the other hand, is used as a preprocessing step to handle high-rank tensors. These methods have shown promise in achieving efficient tensor contractions.
Reinforcement Learning and Graph Neural Networks
Reinforcement learning (RL) combined with graph neural networks (GNNs) is another approach to finding efficient tensor contraction paths. RL algorithms learn from experience to make optimal decisions, while GNNs leverage the power of neural networks to analyze and process graph-structured data. This combination has been applied to both real and synthetic quantum circuits with promising results.
While these existing methods have made significant contributions to enhancing tensor contraction paths, there is still room for improvement. This is where the modified standard greedy algorithm with an improved cost function comes into play.
Introducing the Modified Standard Greedy Algorithm
A team of researchers has introduced a novel method to enhance tensor contraction paths using a modified standard greedy algorithm with an improved cost function. The standard greedy algorithm (SGA) is widely used to find pairwise contractions for the path at each step. However, the cost function used by SGA is straightforward and depends solely on the sizes of the input and output tensors.
The proposed method overcomes this limitation by introducing a modified cost function that takes into account additional information. Instead of relying on a single cost function, the modified greedy algorithm incorporates multiple cost functions at runtime. This allows for a broader range of problems to be addressed and improves the efficiency of tensor contraction paths.
To evaluate the effectiveness of the modified algorithm, the researchers compared it against state-of-the-art greedy implementations by Optimized Einsum (opt_einsum). The results showed that the proposed method outperformed opt_einsum in terms of computational efficiency. Additionally, in some cases, the modified algorithm even outperformed methods like hypergraph partitioning combined with greedy.
Three Phases of Computing Contraction Paths
The modified greedy algorithm follows three phases to compute tensor contraction paths more efficiently:
- Initialization: In this phase, the algorithm initializes the cost function parameters and selects an appropriate cost function based on the problem at hand.
- Recursive Expansion: The modified algorithm explores tensor contraction paths recursively. At each step, it evaluates different cost functions and selects the one that yields the best contraction.
- Termination: The algorithm terminates when it has computed the desired number of contraction paths or when it reaches a specified computation time limit.
By using cost functions as parameters and dynamically selecting the most appropriate cost function at runtime, the modified greedy algorithm achieves more efficient tensor contraction paths.
Experimental Evaluation and Results
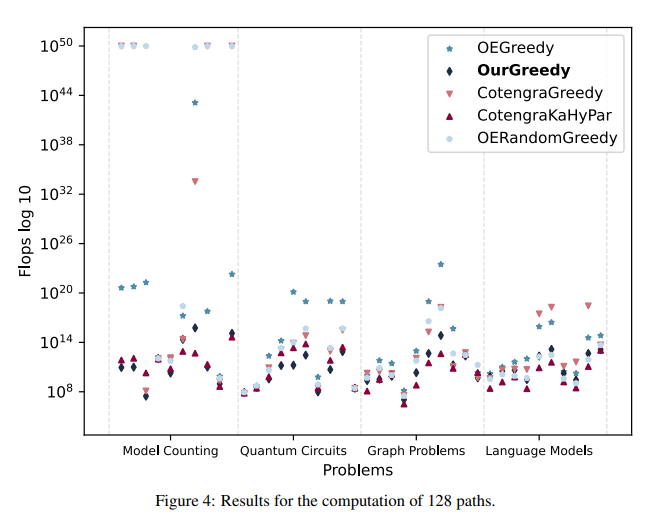
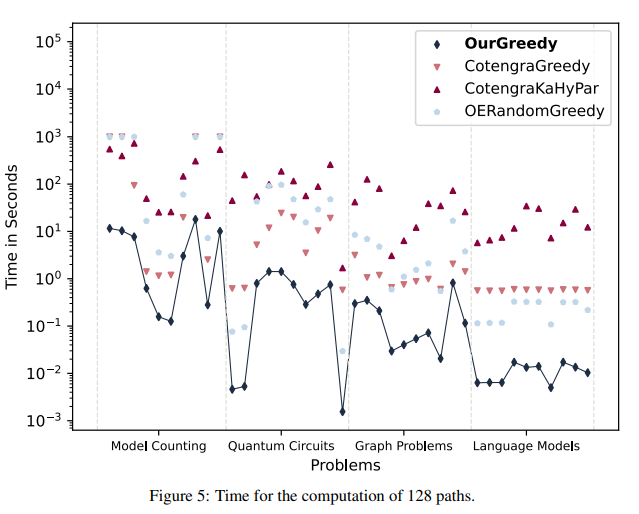
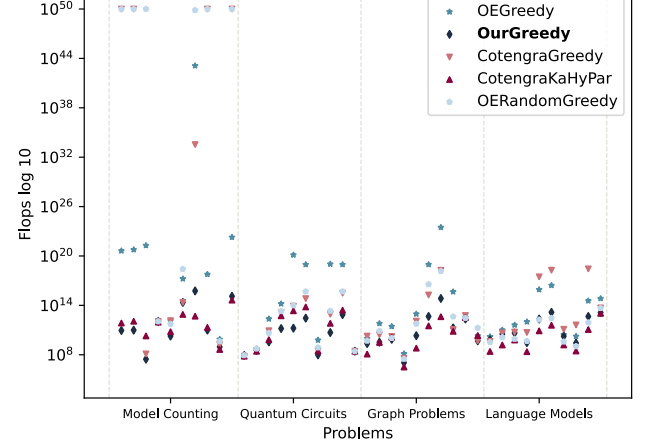
To assess the performance of the proposed method, the researchers conducted experiments comparing it with other algorithms. They computed tensor contraction paths for 10 different problems and measured the flops (floating-point operations) for each algorithm.
Two experiments were performed to evaluate the method’s quality and efficiency:
- Solution Quality: In this experiment, the algorithms computed 128 paths for each problem example, without considering computation time. This allowed the researchers to assess the solution’s quality.
- Time and Quality Trade-off: The second experiment imposed a computation time limit of 1 second. The goal was to strike a balance between time and quality, finding an efficient path quickly for practical scenarios.
The results of the experiments demonstrated that the proposed method achieved efficient tensor contraction paths in less time and successfully solved complex problems. The modified algorithm outperformed standard greedy and random greedy algorithms by opt_einsum, as well as the greedy algorithm and hypergraph partitioning method.
Conclusion
In conclusion, enhancing tensor contraction paths is a critical aspect of optimizing computational efficiency in various research fields. The use of a modified standard greedy algorithm with an improved cost function offers a promising approach to achieving more efficient tensor contractions.
By incorporating multiple cost functions and dynamically selecting the most appropriate one at runtime, the modified algorithm outperforms existing methods in terms of computational efficiency. The experimental evaluation showcases its effectiveness in solving complex problems with shorter computation times.
The proposed method opens up new avenues for further research and optimization of tensor contraction paths. With ongoing advancements in algorithms and computational techniques, we can expect even more efficient tensor contractions in the future.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on LinkedIn. Do join our active AI community on Discord.
Explore 3600+ latest AI tools at AI Toolhouse 🚀.
If you like our work, you will love our Newsletter 📰