How a 1960s Matrix Normalization Method Helped DeepSeek Stabilize Next-Generation Language Models with mHC
Large language models have grown deeper, wider, and more complex over the last decade. Each architectural leap has unlocked new performance gains, but often at the cost of training instability and rising system overhead. One such leap was the introduction of hyper connections, a generalization of residual connections designed to increase expressivity without a linear explosion in parameters. While promising, hyper connections created a new and serious problem at scale: numerical instability.
In a recent breakthrough, DeepSeek researchers revisited a classical algorithm from 1967, the Sinkhorn–Knopp matrix normalization method, and applied it in a modern deep learning context. By constraining how information is mixed across residual streams, they restored stability while preserving the benefits of richer network topology. This approach, called Manifold Constrained Hyper Connections (mHC), offers a compelling example of how classical mathematics can solve modern AI challenges.
This article explains the problem hyper connections introduced, why instability arises in deep networks, and how a decades old matrix normalization algorithm provides an elegant and effective fix.
From Residual Connections to Hyper Connections
Residual connections were a turning point in deep learning. They made it possible to train very deep networks by ensuring that information and gradients could flow through layers without vanishing or exploding. In its simplest form, a residual update looks like:
xₗ₊₁ = xₗ + F(xₗ, Wₗ)
The identity path ensures that even if the transformation F is imperfect, the signal magnitude remains controlled.
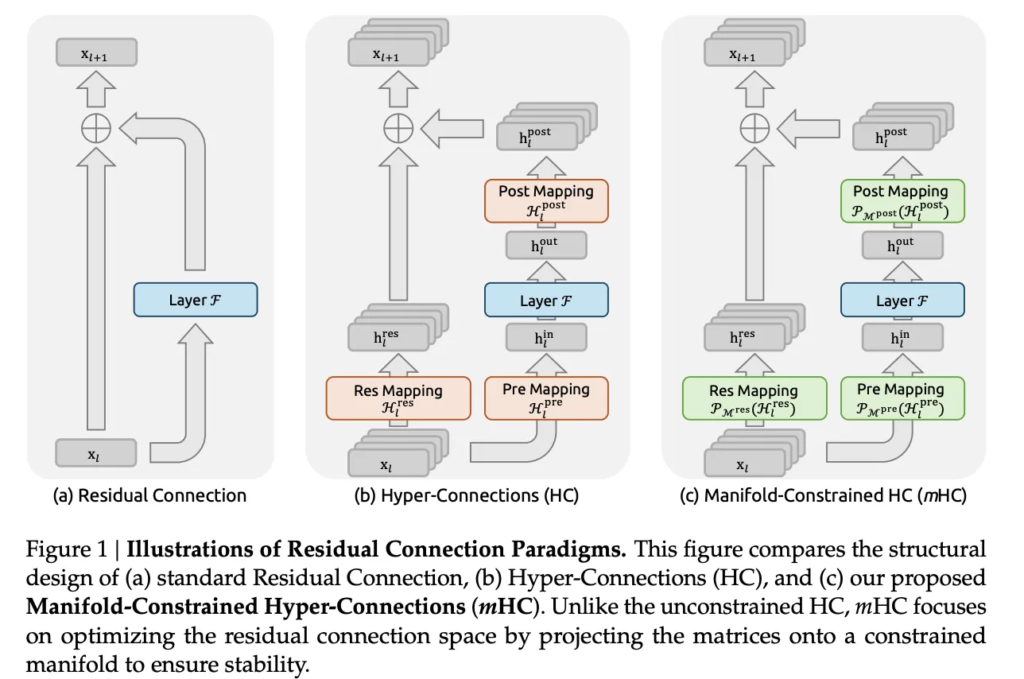
Hyper connections extend this idea by widening the residual pathway. Instead of a single residual vector, the network maintains multiple parallel residual streams. At each layer, the model learns how to read from these streams, apply transformations, and write results back into the buffer. This design increases representational capacity without dramatically increasing floating point operations, which is why hyper connections showed improved downstream performance in large language models.
However, widening the residual stream also introduces a new degree of freedom. Instead of passing information through a near identity mapping, the model learns a residual mixing matrix that combines streams across layers. Over dozens or hundreds of layers, these matrices multiply together, and that is where the trouble begins.
Why Hyper Connections Become Unstable
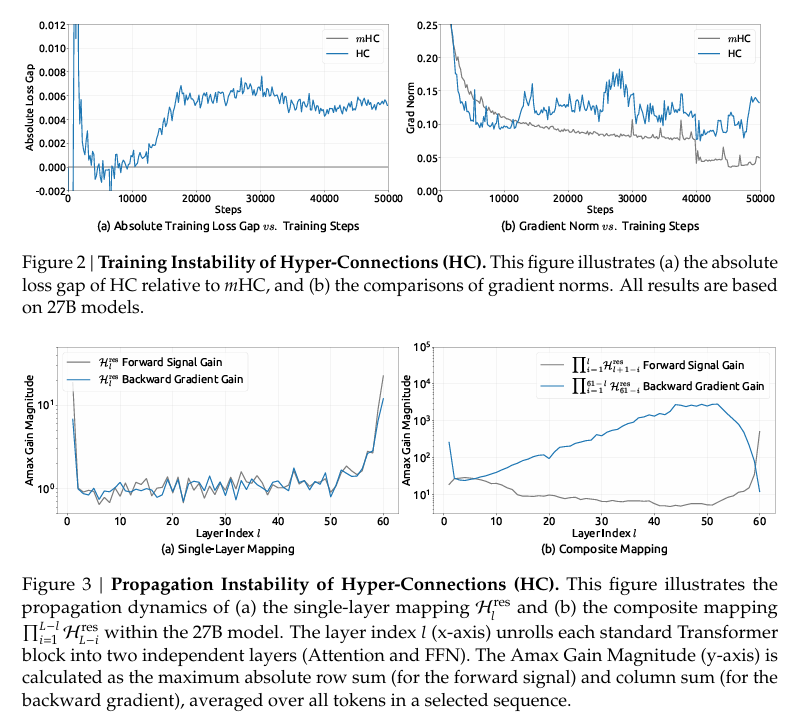
DeepSeek researchers analyzed the composite effect of residual mixing across many layers in large mixture of experts models. They introduced a metric called Amax Gain Magnitude, which measures worst case signal amplification based on maximum row and column sums of the combined residual mapping.
In an ideal residual network, this gain stays close to 1. That means signals neither explode nor vanish as they propagate forward or backward. In unconstrained hyper connection models, the picture was dramatically different. In a 27 billion parameter model, the gain magnitude spiked to values near 3000, indicating severe amplification.
Practically, this manifested as training instabilities, sudden loss spikes, and highly erratic gradient norms. Even small deviations in the learned mixing matrices compounded exponentially with depth. While hyper connections improved expressivity, they undermined the very property that made residual networks reliable.
This instability also made naive scaling unattractive for production models. Multi stream buffers increased memory traffic per token, and without guarantees on numerical behavior, training became risky and expensive.
Revisiting a 1967 Algorithm
The key insight behind mHC was that the instability came from unconstrained residual mixing. If the mixing matrices could be forced to behave more like identity mappings, while still allowing cross stream communication, the problem might disappear.
To achieve this, DeepSeek researchers constrained each residual mixing matrix to lie on a specific mathematical manifold: the set of doubly stochastic matrices, also known as the Birkhoff polytope. A doubly stochastic matrix has three properties:
- All entries are non negative
- Each row sums to 1
- Each column sums to 1
Such matrices represent convex combinations of permutation matrices. In intuitive terms, they mix streams by averaging rather than amplifying, ensuring that total signal mass is preserved.
To project arbitrary matrices onto this manifold, the team used the Sinkhorn–Knopp algorithm, introduced in 1967. The algorithm alternates between normalizing rows and columns until the matrix approximately satisfies the doubly stochastic constraints. This alternating normalization converges reliably under mild conditions.
Manifold Constrained Hyper Connections Explained
In the mHC architecture, the residual mixing matrix at each layer is no longer free to take arbitrary values. Instead, after being parameterized, it is projected onto the Birkhoff polytope using a fixed number of Sinkhorn–Knopp iterations.
In practice, DeepSeek uses around 20 iterations per layer, which is sufficient to keep the matrix close to doubly stochastic while keeping computational cost manageable.
Under these constraints:
- Residual mixing becomes a convex combination of streams
- Feature magnitudes are preserved across layers
- Long range signal propagation remains stable
The researchers also ensure that input and output mixing coefficients are non negative, avoiding destructive cancellation between streams. The result is a residual pathway that behaves like a generalized identity mapping rather than an uncontrolled amplifier.
Quantitative Stability Gains
The effect of this constraint is dramatic. In the same 27 billion parameter model where unconstrained hyper connections produced gain magnitudes near 3000, mHC kept the Amax Gain Magnitude bounded around 1.6.
This represents a reduction of roughly three orders of magnitude in worst case amplification. More importantly, it restores the core property that made residual connections successful in the first place: predictable signal flow across deep stacks.
Unlike heuristic fixes or aggressive regularization, this stability comes directly from a mathematical constraint. The architecture itself enforces norm control, rather than relying on training tricks.
Systems Design and Training Overhead
At first glance, applying Sinkhorn–Knopp normalization at every layer might seem prohibitively expensive. DeepSeek addressed this with careful systems engineering.
Key optimizations include:
- Fused kernels that combine normalization, projection, and gating operations to minimize memory traffic
- Activation recomputation strategies that trade extra compute for reduced memory footprint during backpropagation
- Pipeline aware scheduling, similar to DualPipe approaches, that overlaps communication with recomputation
With these optimizations in place, mHC with a residual expansion factor of four added only about 6.7 percent training time overhead compared to the baseline architecture.
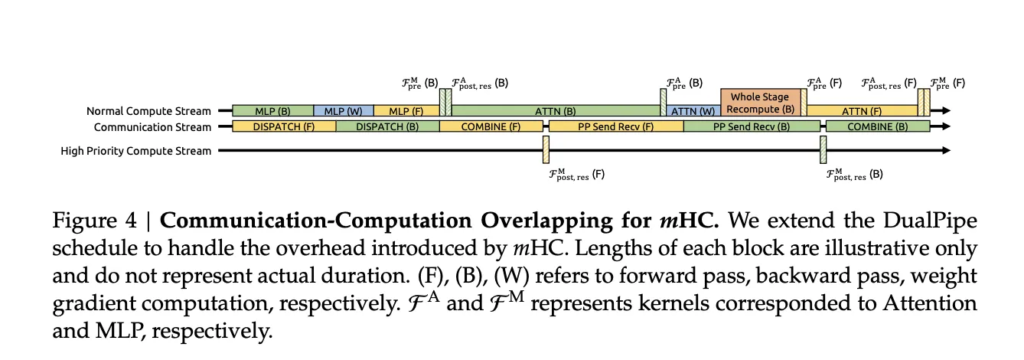
Given the stability and performance gains, this overhead is modest and predictable, making mHC viable for large scale training.
Empirical Performance Improvements
Stability alone would justify mHC, but the approach also delivers measurable accuracy gains. DeepSeek evaluated 3B, 9B, and 27B mixture of experts models across standard language model benchmarks such as BBH, DROP, GSM8K, and others.
The pattern was consistent:
- Baseline residual models performed worst
- Hyper connections improved performance but were unstable
- mHC delivered the best results while remaining stable
For example, on the BBH benchmark, a 27B model improved from 43.8 with standard residuals to 48.9 with hyper connections, and further to 51.0 with mHC. Similar gains were observed on DROP and other tasks.
These results suggest that constraining residual topology does not limit expressivity. Instead, it enables the model to fully exploit richer connections without collapsing during training.
Why This Matters for the Future of LLMs
Most scaling strategies in large language models focus on increasing parameter count, context length, or dataset size. mHC introduces a different axis of scaling: residual topology design.
By explicitly shaping how information flows through deep networks, researchers can unlock new forms of expressivity without sacrificing stability. The success of mHC also highlights an important lesson: some of the most effective innovations come from revisiting classical ideas and applying them in new contexts.
The Sinkhorn–Knopp algorithm was never designed with transformers or mixture of experts models in mind. Yet, nearly sixty years later, it provides a clean and principled solution to one of the most pressing problems in modern deep learning.
Key Takeaways
- Hyper connections increase model expressivity but introduce severe training instability at scale
- Instability arises from unconstrained residual mixing across deep stacks
- DeepSeek constrains residual mixers to the manifold of doubly stochastic matrices
- A 1967 algorithm, Sinkhorn–Knopp normalization, enforces this constraint efficiently
- Worst case signal amplification drops from around 3000 to about 1.6
- The approach improves benchmark performance with only modest training overhead
- mHC opens a new direction for scaling LLMs through structured residual design
By blending classical mathematics with modern systems engineering, DeepSeek’s work demonstrates that architectural rigor can be as powerful as brute force scaling. As models continue to grow, such principled approaches are likely to play a central role in the next generation of large language models.
Check out the full paper here. All credit for this news goes to the researchers of this project. Explore one of the largest MCP directories created by AI Toolhouse, containing over 4500+ MCP Servers: AI Toolhouse MCP Servers Directory