New Stochastic Methods Enhance RL Performance in Large Action Spaces
Reinforcement learning (RL) has revolutionized the field of artificial intelligence by enabling agents to learn and make decisions through interaction with their environment. However, traditional RL methods struggle to handle environments with large discrete action spaces due to computational limitations. Recent research from KAUST and Purdue University addresses this challenge by presenting efficient stochastic methods that improve the scalability and performance of RL in such environments.
The Challenge of Large Discrete Action Spaces
In RL, an agent learns to maximize its cumulative reward by taking actions in an environment and observing the resulting feedback. The agent’s goal is to find the optimal policy that guides its decision-making process. Q-learning, a popular RL algorithm, estimates the value of each state-action pair and updates the agent’s policy accordingly. However, as the number of actions grows, Q-learning becomes computationally expensive, making it impractical for real-world applications.
Consider a scenario where an RL agent controls a robotic arm with thousands of possible actions. Evaluating the value of each action at every decision point becomes infeasible, leading to inefficiencies and limitations in decision-making. Traditional RL methods struggle to scale in such environments, hindering their practical use in complex real-world scenarios.
Introducing Stochastic Methods for Efficient RL
To address the challenges posed by large discrete action spaces, researchers from KAUST and Purdue University have introduced efficient stochastic methods for RL. These methods aim to reduce computational complexity while maintaining high performance, making RL more practical and effective in complex environments.
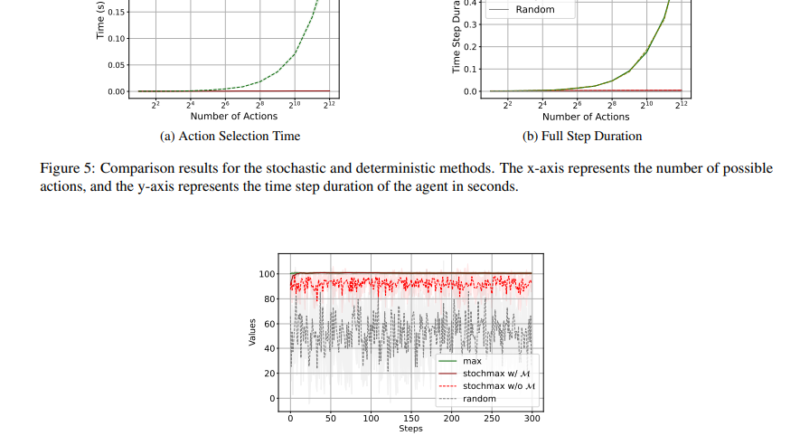
The researchers presented several stochastic value-based RL methods, including Stochastic Q-learning, StochDQN, and StochDDQN. These methods leverage stochastic maximization techniques to alleviate the computational burden of evaluating all possible actions at each decision point. By considering only a subset of actions in each iteration, these methods achieve significant computational savings without sacrificing performance.
Stochastic Q-Learning
Stochastic Q-learning is an extension of traditional Q-learning that incorporates stochastic maximization techniques. Instead of evaluating the value of all possible actions, Stochastic Q-learning considers a subset of actions sampled stochastically. This approach allows the algorithm to converge faster and handle large discrete action spaces more efficiently.
The researchers conducted a theoretical analysis of Stochastic Q-learning and proved its convergence properties. The algorithm showed promising results in various environments, including Gymnasium environments like FrozenLake-v1 and MuJoCo control tasks such as InvertedPendulum-v4 and HalfCheetah-v4.
StochDQN and StochDDQN
StochDQN and StochDDQN are stochastic extensions of deep Q-networks (DQN), a popular RL algorithm that employs neural networks to approximate value functions. These stochastic methods replace the traditional max and arg max operations with stochastic equivalents, reducing the computational complexity of evaluating numerous actions.
The researchers evaluated StochDQN and StochDDQN on different datasets and environments. In the FrozenLake-v1 environment, StochDQN achieved optimal cumulative rewards in 50% fewer steps compared to traditional DQN, demonstrating its improved efficiency. Similarly, StochDDQN outperformed DDQN in the HalfCheetah-v4 task, completing 100,000 steps in just 2 hours compared to DDQN’s 17 hours. These results highlight the effectiveness of stochastic methods in reducing computational time and improving RL performance.
Benefits and Implications
The introduction of efficient stochastic methods for RL in large discrete action spaces offers several benefits and implications. Firstly, these methods provide scalable solutions for real-world applications where quick and effective decision-making is crucial. By significantly reducing computational complexity, RL agents can make decisions in complex environments more efficiently.
Secondly, the stochastic methods presented by KAUST and Purdue University improve the convergence speed of RL algorithms. Faster convergence allows RL agents to learn optimal policies more quickly, which is essential for time-sensitive applications.
Thirdly, the efficiency of stochastic methods enables RL agents to handle environments with a large number of actions. This capability broadens the applicability of RL in various domains, including robotics, autonomous vehicles, and strategic game-playing technologies.
Conclusion
The KAUST and Purdue University research paper presents efficient stochastic methods for RL in large discrete action spaces. These methods, including Stochastic Q-learning, StochDQN, and StochDDQN, leverage stochastic maximization techniques to reduce computational complexity while maintaining high performance.
The experiments conducted on different datasets and environments demonstrate the superiority of stochastic methods over traditional RL algorithms. Stochastic Q-learning, StochDQN, and StochDDQN achieve faster convergence and higher efficiency, handling up to 4096 actions with significantly reduced computational time per step.
The innovations presented in this research hold significant potential for advancing RL technologies in diverse fields. By addressing the challenge of large discrete action spaces, these efficient stochastic methods make RL more practical and effective in complex environments. Future research and application of these methods can further enhance the capabilities of RL agents and contribute to the advancement of AI.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on LinkedIn. Do join our active AI community on Discord.
Explore 3600+ latest AI tools at AI Toolhouse 🚀.
If you like our work, you will love our Newsletter 📰