Enhancing Graph Data Embeddings with Machine Learning: The Deep Manifold Graph Auto-Encoder (DMVGAE/DMGAE) Approach
Graph data is becoming increasingly prevalent in various domains such as social networks, recommendation systems, and bioinformatics. The ability to effectively represent and analyze graph data is crucial for extracting meaningful insights and making informed decisions. In recent years, machine learning techniques have been applied to enhance graph data embeddings, enabling more accurate and efficient analysis. One such approach is the Deep Manifold Graph Auto-Encoder (DMVGAE/DMGAE) approach, which combines manifold learning and auto-encoder-based techniques to improve the quality of graph data embeddings.
🔥Explore 3500+ AI Tools and 2000+ GPTs at AI Toolhouse
Understanding Manifold Learning and Auto-Encoders
Before delving into the DMVGAE/DMGAE approach, it is essential to understand the concepts of manifold learning and auto-encoders.
Manifold learning is based on the manifold assumption, which posits that high-dimensional data lies on a lower-dimensional manifold within the ambient space [1]. In other words, manifold learning techniques aim to uncover the underlying structure or patterns in the data by reducing its dimensionality. This is particularly useful when dealing with complex data, such as graphs, where traditional linear dimensionality reduction techniques may not be effective.
Auto-encoders, on the other hand, are neural networks that are trained to reconstruct their input data. They consist of an encoder network that maps the input data to a lower-dimensional representation (encoding) and a decoder network that reconstructs the original data from the encoded representation. By learning to reconstruct the input data, auto-encoders can capture informative features and representations of the data [4].
The Deep Manifold Graph Auto-Encoder (DMVGAE/DMGAE) Approach
The DMVGAE/DMGAE approach combines the principles of manifold learning and auto-encoders to enhance graph data embeddings. This approach aims to preserve the topological structure and distances between nodes in the graph while learning a low-dimensional representation.
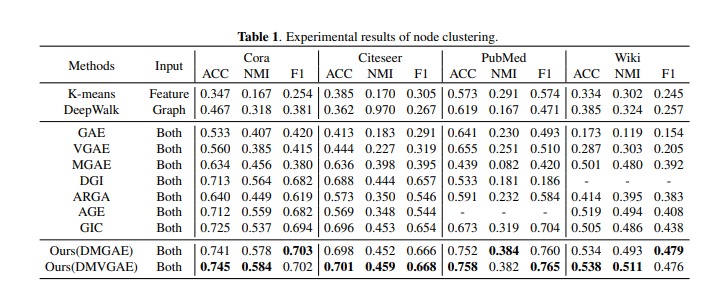
The researchers at Zhejiang University propose the DMVGAE/DMGAE method for attributed graph embedding [2]. The key idea behind this approach is to transform the problem of preserving structure information into maintaining inter-node similarity between the non-Euclidean, high-dimensional latent space and the Euclidean input space.
To achieve this, the DMVGAE/DMGAE approach employs a variational autoencoder mechanism. Variational autoencoders are a variant of autoencoders that learn the distribution of the latent space instead of directly mapping the input data to a fixed encoding [5]. By modeling the distribution of the latent space, the DMVGAE/DMGAE approach can generate more expressive and robust embeddings.
In addition to the variational autoencoder mechanism, the DMVGAE/DMGAE approach introduces a graph geodesic similarity to capture the graph’s structural and node feature information. The geodesic similarity measures the similarity between nodes in both the original and latent spaces, taking into account the graph’s topological structure [2]. A t-distribution is used as a kernel function to balance the intra-cluster and inter-cluster relationships, effectively capturing the complex relationships within the graph.
By effectively combining manifold learning and auto-encoder-based techniques, the DMVGAE/DMGAE approach achieves significant improvements in the stability and quality of graph data embeddings. Experimental results on various benchmark tasks demonstrate the state-of-the-art performance of the proposed method [2].
Conclusion
Enhancing graph data embeddings with machine learning techniques is essential for effectively analyzing and extracting insights from graph data. The Deep Manifold Graph Auto-Encoder (DMVGAE/DMGAE) approach combines manifold learning and auto-encoder-based techniques to improve the stability and quality of graph data embeddings.
By leveraging the principles of manifold learning, the DMVGAE/DMGAE approach uncovers the underlying structure and patterns in the graph data. The variational autoencoder mechanism enables the learning of expressive and robust embeddings by modeling the distribution of the latent space. The introduction of graph geodesic similarity captures the graph’s topological structure and node feature information, further enhancing the quality of the embeddings.
The DMVGAE/DMGAE approach has shown promising results in various benchmark tasks, outperforming state-of-the-art baseline algorithms. Its ability to preserve inter-node similarity and capture complex relationships within the graph makes it a valuable tool in graph analysis and other related domains.
As the field of machine learning continues to advance, further research and development in enhancing graph data embeddings are expected. The DMVGAE/DMGAE approach sets the stage for future innovations in this area, and its effectiveness makes it a promising technique for real-world applications.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on LinkedIn. Do join our active AI community on Discord.
If you like our work, you will love our Newsletter 📰